
 |
 |
 |
 |
| Главная
:: Математические знаки
Математические знаки Попробуйте показать иностранцу, не знакомому с русским языком,
запись "Ваня + Аня = Любовь". Он, наверняка, поймет только два
символа: "+" и "=". Точно так же мы узнаем эти символы в японском
эквиваленте: Первыми математическими знаками были цифры. Наиболее удобными
оказались арабские цифры: 0, 1, 2 и т.д. Римскими цифрами пользуются
достаточно редко: иногда ими записывают века и года (MMI=2001
год), главы книг или нумерованные события (XXIV съезд КПСС). Буквенные
обозначения для неизвестных величин появилось еще в III веке у
Диофанта. Он же ввел особые знаки для арифметических операций.
Однако, только к XIV - XVII вв. была создана система буквенных
обозначений, характерная для наших дней. В конце XV века итальянец
Л. Пачоли и француз Н. Шюке для сложения и вычитания применили
знаки
Дж. Кардано (1545 г.) записал бы в виде I.cubus . 3.positionibus aequantur 14 (cubus - куб, positio - неизвестная, aequantur - равно). Француз Ф.Виет (1591 г.) записал бы его как IC. + 3N aequantur 14 Но уже в 1631г. англичанин Т. Гарриот использовал бы для записи этого уравнения вполне понятный для нас вид aaa+3a = 14 Р. Декарт в 1637 г. придал алгебраическим выражениям полностью современный вид. Он изображал неизвестные величины последними латинскими буквами: x, y, z, а параметры - начальными буквами a, b, c. Постепенно принимали знакомый всем вид показатели степеней и
знаки радикала. Последний знак состоит из двух частей: Уже в XVII в. в первую очередь усилиями Г. Лейбница и И. Ньютона
начали развиваться дифференциальное и интегральное исчисления.
Лейбниц впервые ввел название "производная" ("derivative") в 1667
году : "Aequationem differentialem voco talem qua valor ipsius
dx exprimitur, quaeque ex alia derivata est, qua valor
ipsius x exprimebatur" [cf. page 156 of Leibniz' "Mathematische
Schriften," vol. I, edited by C. I. Gerhardt, Verlag von A. Asher
& Comp., Berlin, 1849]. Он использовал обозначения dx,
dy, Лейбниц начал с обозначения omn. ( = "omnia") как знака
интеграла. Он же ввел и Для определенного интеграла Л. Эйлер предложил пределы интегрирования
заключать в скобки: (a, b) - не привилось! Современная запись
Ну а в последнее время особо новых математических обозначений не вводилось: так что дерзайте! В.В. Калинин
|
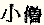 +
+ 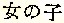 =
=  . Впрочем, не только эти, но и остальные
математические знаки, вполне интернациональны и, практически не
зависят от языка, используемого в той или иной стране. Оставим
для филологов вопрос об исторических предпосылках универсальности
математических обозначений в разных языках. Очевидно впрочем,
что языки возникли гораздо раньше математической нотации. Может,
человечество к семнадцатому столетию от Рождества Христова осознало,
что хотя бы в математике не должно быть ни национальных, ни этнических,
ни религиозных, ни классовых различий. А все-таки, как же и когда
возникли современные символы математики.
. Впрочем, не только эти, но и остальные
математические знаки, вполне интернациональны и, практически не
зависят от языка, используемого в той или иной стране. Оставим
для филологов вопрос об исторических предпосылках универсальности
математических обозначений в разных языках. Очевидно впрочем,
что языки возникли гораздо раньше математической нотации. Может,
человечество к семнадцатому столетию от Рождества Христова осознало,
что хотя бы в математике не должно быть ни национальных, ни этнических,
ни религиозных, ни классовых различий. А все-таки, как же и когда
возникли современные символы математики. 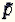 (от латинского plus)
и
(от латинского plus)
и 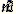 (minus), а немецкие математики применили современные
обозначения + и - . В XVI в. использовалась смешанная запись,
содержащая и слова и некоторые математические знаки. Так, уравнение
(minus), а немецкие математики применили современные
обозначения + и - . В XVI в. использовалась смешанная запись,
содержащая и слова и некоторые математические знаки. Так, уравнение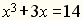
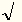 - модифицированная буква
r (от radix - "корень") и черта, заменявшая скобки.
- модифицированная буква
r (от radix - "корень") и черта, заменявшая скобки.
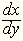 . А еще через сотню лет
Ж. Лагранж ввел очень удобную запись, который мы и пользуемся
поныне:
. А еще через сотню лет
Ж. Лагранж ввел очень удобную запись, который мы и пользуемся
поныне: 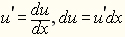 . Термин "дифференциал" на английском языке
появилось в 1704 году в "Lexicon technicum" - универсальном словаре
искусства и науки Джона Харриса.
. Термин "дифференциал" на английском языке
появилось в 1704 году в "Lexicon technicum" - универсальном словаре
искусства и науки Джона Харриса.  современное как стилизованную букву S (от слова
"summa"). Ньютону повезло меньше: предложенное им для интеграла
обозначение
современное как стилизованную букву S (от слова
"summa"). Ньютону повезло меньше: предложенное им для интеграла
обозначение 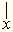 было отвергнуто, так как
очень походило на "штрих". Само название "Интеграл" в печати
первым дал Якоб Бернулли в 1690 году: "Ergo et horum Integralia
aequantur" (Cajori vol. 2, page 182; Ball). Однако, другой представитель
этой славной семьи, Иоганн, также претендовал на первенство в
использовании термина. К слову сказать, семья Бернулли - три поколения
- внесла огромный вклад в современные науки: математику, физику,
химию. И сейчас, отдавая им за это должное, уже никто не интересуется,
кто конкретно из них за что отвечает. О важности понятия интеграла
знал даже Лев Толстой: "Когда бы в университете мне сказали, что
другие понимают интегральное вычисление, а я не понимаю, - тут
самолюбие. Но тут надо быть убежденным прежде, что нужно иметь
известные способности для этих дел и, главное, в том, что все
эти дела важны очень." ("Анна Каренина".)
было отвергнуто, так как
очень походило на "штрих". Само название "Интеграл" в печати
первым дал Якоб Бернулли в 1690 году: "Ergo et horum Integralia
aequantur" (Cajori vol. 2, page 182; Ball). Однако, другой представитель
этой славной семьи, Иоганн, также претендовал на первенство в
использовании термина. К слову сказать, семья Бернулли - три поколения
- внесла огромный вклад в современные науки: математику, физику,
химию. И сейчас, отдавая им за это должное, уже никто не интересуется,
кто конкретно из них за что отвечает. О важности понятия интеграла
знал даже Лев Толстой: "Когда бы в университете мне сказали, что
другие понимают интегральное вычисление, а я не понимаю, - тут
самолюбие. Но тут надо быть убежденным прежде, что нужно иметь
известные способности для этих дел и, главное, в том, что все
эти дела важны очень." ("Анна Каренина".) 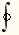 была введена Ж. Фурье в 1822 г., а обозначение
была введена Ж. Фурье в 1822 г., а обозначение
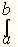 для интеграла по контуру ввел в 1917 г. Зоммерфельд,
что привело, как нам известно, к революции в России (шучу - В.К.).
Знак предела в виде
для интеграла по контуру ввел в 1917 г. Зоммерфельд,
что привело, как нам известно, к революции в России (шучу - В.К.).
Знак предела в виде 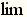 (с точкой) предложил Люилье в 1786 г.,
обозначение
(с точкой) предложил Люилье в 1786 г.,
обозначение 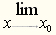 - это заслуга Харди (1908
г.) Привычное обозначение для частной производной
- это заслуга Харди (1908
г.) Привычное обозначение для частной производной 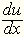 впервые ввел Лежандр
в 1786 г. Правда, ему это почему-то не понравилось и эта запись
не использовалась вплоть до 1841 г. у Якоби.
впервые ввел Лежандр
в 1786 г. Правда, ему это почему-то не понравилось и эта запись
не использовалась вплоть до 1841 г. у Якоби.